数値流体力学
埋め込み境界法による空力音の直接数値解法の開発
航空機のジェットエンジンや新幹線のような高速鉄道車両は大きな騒音を発生します。その主な成分は空気力学的に発生する空力音です。空力騒音を低減するためには、その発生原因を知ることが重要です。われわれは直接数値シミュレーションにより空力音解析に取り組んでいます。
騒音は大きいものであってもその圧力変動は大気圧に比べると小さい(120dBの騒音でも0.02%程度)ので、流体力学の方程式の解として音を捉える直接数値シミュレーションには高い精度が求められます。また、空力騒音を発生する系には複雑な形状の物体や、運動する物体が含まれていることが多いです。本研究では、高精度解法と埋め込み境界法を両立させることでこの二つの課題を解決しました。従来の手法で解ける問題について本研究の手法の精度が十分であることを示し、運動物体と固定された物体を同時に含む流れのような従来の手法では解けなかった問題へ応用できることを示しました。
直接数値シミュレーションは大きな計算機資源(計算速度と主記憶容量)を必要とするため、現在までの計算は小さい系に限られていますが、今後計算機性能の向上により応用範囲が広がることが期待されています。
- Ryu Komatsu, Wakana Iwakami and Yuji Hattori, “Direct numerical simulation of aeroacoustic sound by volume penalization method,” Comput. Fluids 130 (2016) 24-36.
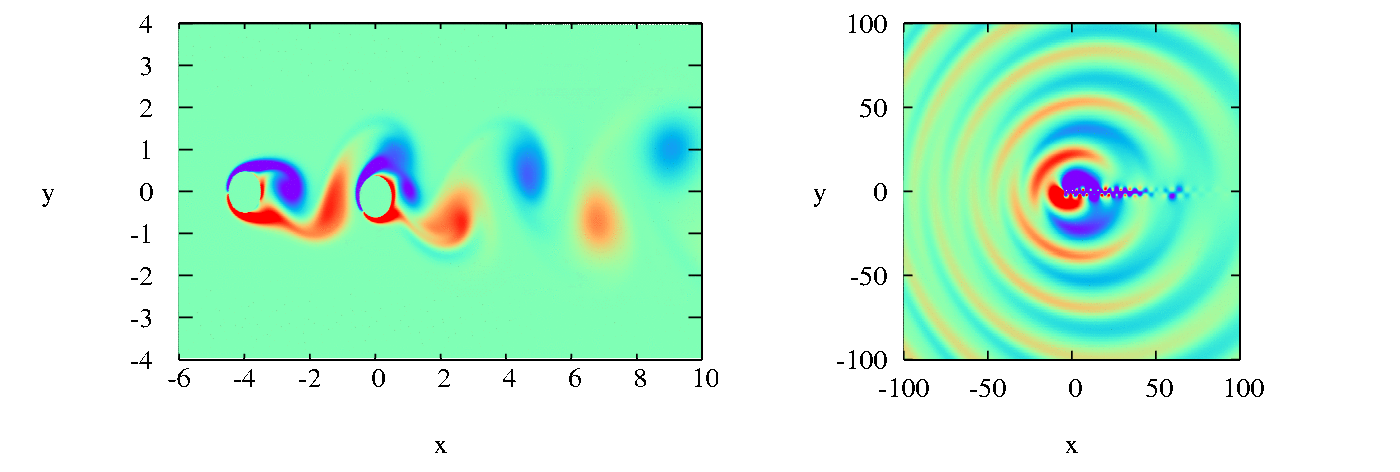
空力騒音
乱流
機械学習による乱流モデルの開発
自然現象や工学機器にあらわれる流れの多くは、乱れた流れ=「乱流」です。乱流を正確に予測することは、自然現象の解明や工学機器の開発のために重要です。乱流の数値シミュレーションには、現在のスーパーコンピューターでも解像しきれない乱れ成分の効果を「乱流モデル」として取り入れますが、より精度の高い乱流モデルが必要とされています。
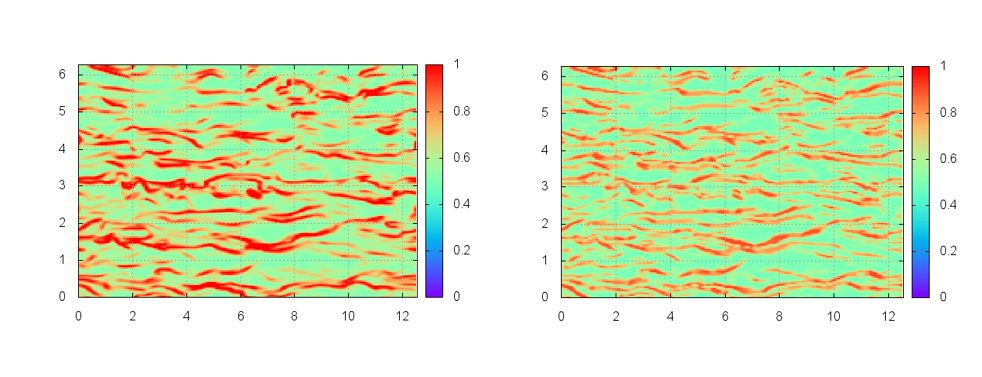
この研究では、機械学習の技術を用いて、ラージ・エディ・シミュレーション(LES)と呼ばれる乱流計算法のための乱流モデルを開発しました。学習のための訓練データは、乱れ成分を正確に捉えられる直接数値シミュレーションにより作成しました。これを用いてニューラルネットワークによる教師あり学習により、解像しきれない乱れ成分の効果を推定できることを示しました。
機械学習の技術は多くの分野に広まっています。乱流研究への応用も急速に増えていて、今後の発展が期待されています。

境界層遷移の抑制による摩擦抵抗低減手法の開発
流れの中に置かれた物体の周りには、境界層と呼ばれる流速の勾配が大きい領域が発生します。境界層が層流から乱流へ遷移すると、物体にかかる摩擦抵抗は急激に大きくなり、例えば航空機全体が受ける抵抗の約半分はこの摩擦抵抗であると言われています。われわれは乱流遷移を抑制して摩擦抵抗を低減する方法を、理論と数値計算によって明らかにしようとしています。
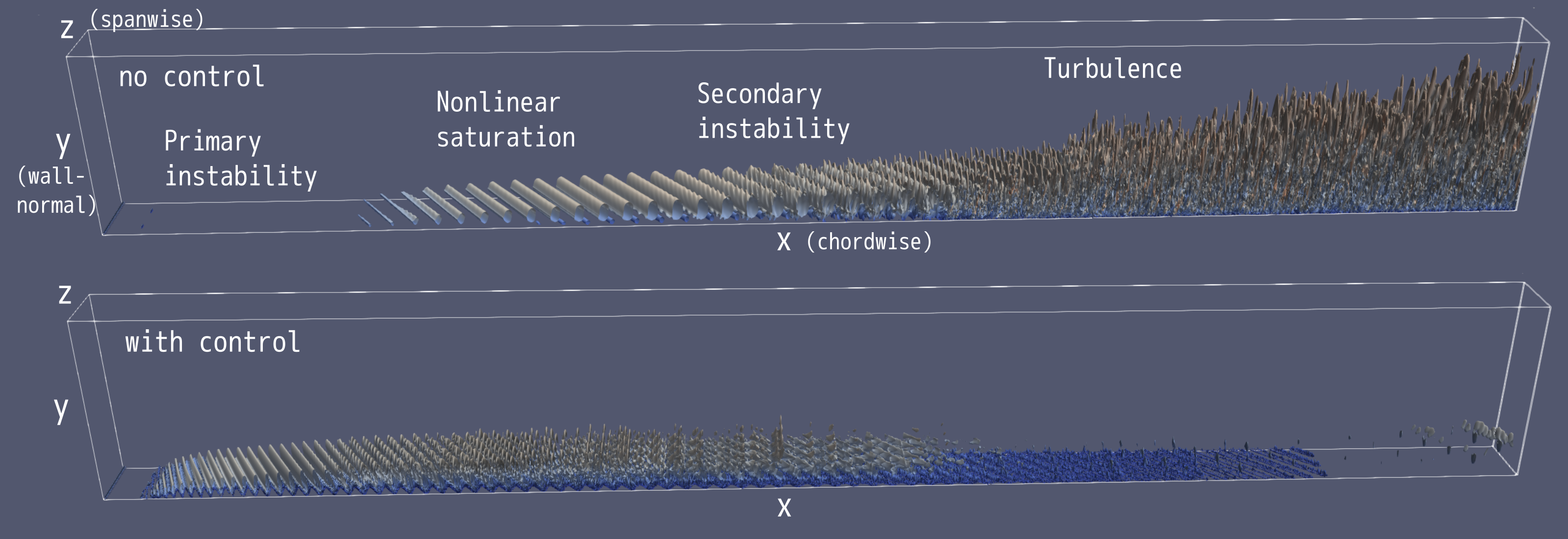
境界層では微小な擾乱が不安定性によって増幅した結果、乱流へと遷移します。よって、境界層における流れの安定性を解析し、不安定性を回避・抑制することが鍵となります。また、物体表面の粗さは特に影響の大きい擾乱源であり、逆に言えば表面に巧妙な隆起構造を設置することで、不安定性の成長を抑制できる可能性があります。本研究では、埋め込み境界法(修正VP法)を応用して特殊な形状の隆起構造を境界層の内部に設置したシミュレーションを行い、航空機の後退翼で発生する横流れ不安定性を抑制できることを示しました。
近年では表面微細加工技術やマイクロ流体制御デバイスも急速に発展してきており、このような遷移制御手法の実用化による航空機の性能向上が現実味を帯びてきています。
- 廣田 真, 井手 優紀, 林田 貴寿, 服部 裕司 "孤立粗度による横流れ不安定性抑制効果の数値的検証" ながれ 38 (2019) 69-72.
- Hirota, M., Hattori, Y., Ide, Y., Takami, H. & Yoshimoto, M. a patent-pending JP2019-069153
渦の動力学
渦輪の曲率不安定性
電磁流体力学
拡張電磁流体力学の理論構築とシミュレーション
プラズマはイオンと電子の二成分からなる電離した気体であり、それぞれが流体方程式に従うだけでなく、電磁場を介して相互作用するのが大きな特徴です。ただし、イオンは電子よりも千倍以上重いため、電子の運動を簡略化した電磁流体力学(MHD)の研究が盛んに行われてきました。近年は計算機性能の向上に伴い、イオンと電子を対等に扱う拡張電磁流体力学の研究が注目を集めており、われわれは数値解法も含めてその基礎的性質の解明に取り組んでいます。
具体的に拡張MHDでは、MHDが無視している電子慣性効果とホール効果が考慮されています。これらは微視的なスケールでしか支配的にならない効果なのですが、実は巨視的な運動にも影響を与えるほど重要であることが明らかになりつつあります。例えば、太陽フレアは磁力線がつなぎ換わることによって磁気エネルギーを一気に解放する爆発現象ですが、本研究では電子慣性を考慮することでその爆発的な傾向が説明できることを示しました。また、このようなエネルギー緩和過程の末に、プラズマ中に生じる自発的な流れや電流の分布を直接数値計算によって調べています。
散逸(粘性や電気抵抗)が小さい無衝突プラズマほど電子慣性やホール効果は無視できず、拡張MHDの研究はこれから宇宙プラズマや高温核融合プラズマなどに応用が進むことが期待されます。
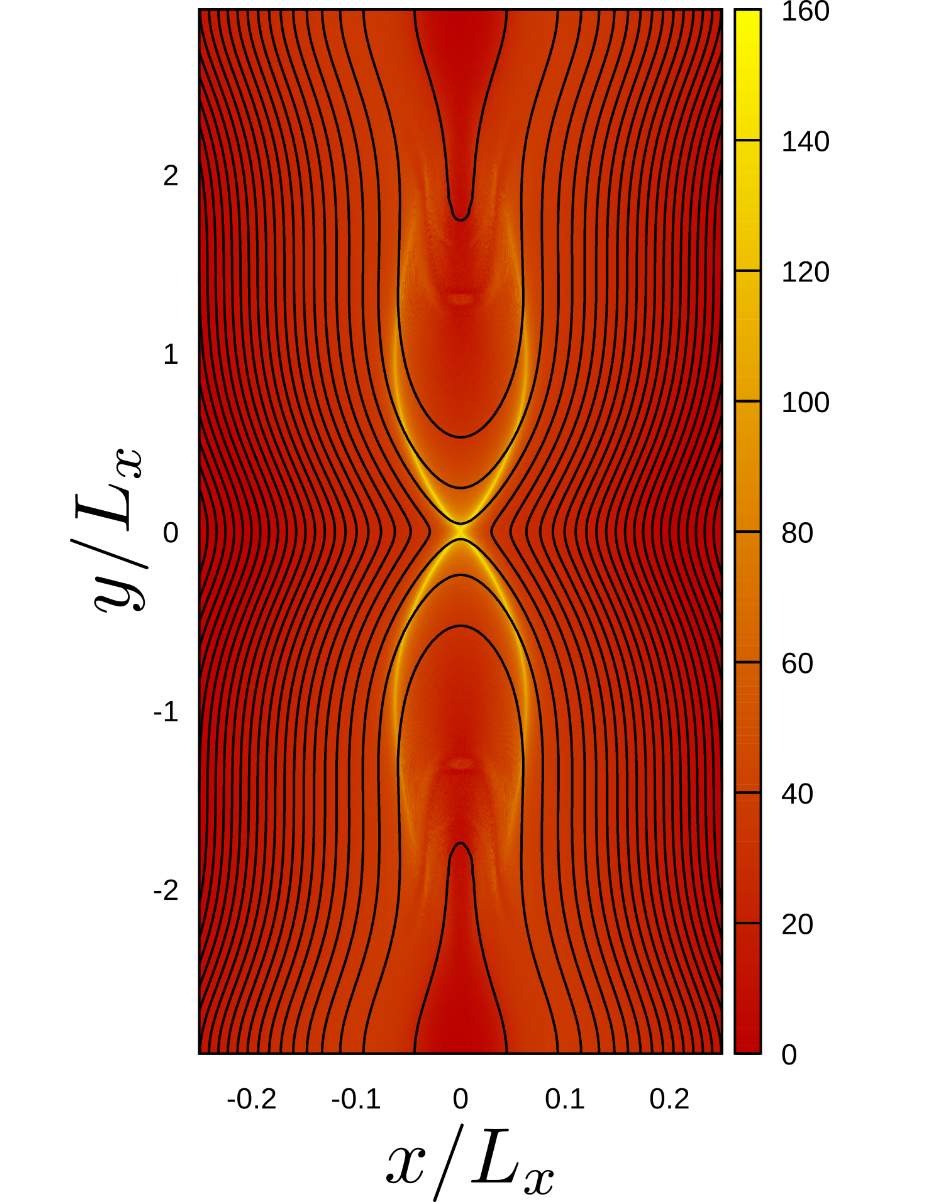
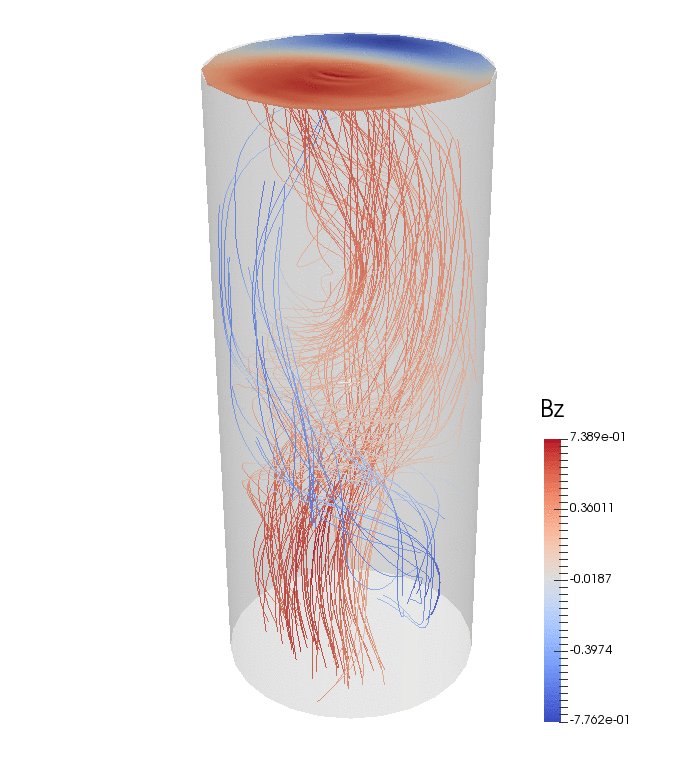
- Makoto Hirota, Yuji Hattori and Philip J Morrison, "Explosive magnetic reconnection caused by an X-shaped current-vortex layer in a collisionless plasma" Physics of Plasmas 22 (2015) 052114.
- Makoto Hirota, "An Explosive Scaling Law for Nonlinear Magnetic Reconnection and Its Insensitivity to Microscopic Scales" Plasma and Fusion Research 12 (2017) 1401010
- 廣田 真, "無衝突プラズマにおける爆発的磁気リコネクションの理論" プラズマ・核融合学会誌 92 (2016) 861-867.
